This page attempts to explain the notions of equation of time and analemma that underlie the elegant curves represented below, familiar to anyone with a passing interest in astronomy. The explanation starts from basic principles and gently introduces necessary astronomical notions along the way. The equation of time and analemma curves for the other planets of the solar system (and Pluto) are shown at the bottom of the page.
The measurement of time
The measurement of time is based on the observation of some periodic (or nearly so) phenomenon chosen as reference. The succession of nights and days and the repetition of the cycle of seasons are two important such phenomena. They still dominate the definition of civil time scales even though the official definition of the second has been based on atomic phenomena since the 1960's (ESAA [1, p. 10]).
Our current model of the universe, based on the ideas of Copernicus, attributes the succession of nights and days to the rotation of the earth on its axis and the cycle of seasons to the revolution of the earth around the sun. However, the facts surrounding the equation of time are directly observable; they do not rely on a particular cosmological model. They were already known in antiquity when the conception of the cosmos was very different.
Celestial sphere and celestial pole
From the point of view of a terrestrial observer, the cloudless sky looks like one half of a sphere of immense radius centered at the observer and to which the celestial objects appear to be attached. This celestial sphere appears to rotate from east to west around a fixed axis, the axis of the world, passing through the observer and the celestial pole, the visible point of the celestial sphere unaffected by the rotation (if the surface of the earth were not in the way, two poles would be visible, opposite to each other with respect to the observer). Objects near the celestial pole, such as the Pole Star in the northern hemisphere, remain almost unaffected by the rotation.
In this model, the succession of nights and days results from the effect on the sun of the rotation of the celestial sphere.
Meridian plane
Each point of the celestial sphere distinct from the poles defines a meridian plane, the half-plane bordered by the axis of the world and containing the point. The meridian plane containing the zenith of the observer (the point of the celestial sphere directly overhead) has special importance, it is called the meridian plane of the observer. It is undefined for an observer at a pole.
The rotation of the celestial sphere can be measured precisely at a particular location on earth by determining the instant of upper culmination (maximum altitude with respect to the horizon) of some reference celestial object on successive days. At that instant, the object lies in the meridian plane of the observer. Any other instant between culminations can be evaluated precisely by measuring the dihedral angle between the meridian plane of the observer and the meridian plane of the reference object.
The angle between two meridian planes can be measured along the celestial equator, the intersection of the celestial sphere and the equatorial plane, perpendicular to the axis of the world through the observer.
Hour angle
The angle between the meridian plane of the observer and the meridian plane of a celestial object, measured from east to west, is called the hour angle of the object. It is measured in hours, minutes, seconds, 24 hours for a whole turn. It increases steadily from one culmination to the next, returning to 0 at each culmination.
Sidereal time
If the reference object is a star or some fixed point of the celestial sphere, then its hour angle is a measure of local sidereal time. The conventional reference point for sidereal time is the vernal point, the point of the celestial equator where the sun lies at the March equinox. In other words, local sidereal time is defined as the hour angle of the vernal point.
Due to the precession of the equinoxes, the vernal point is not strictly speaking a fixed point of the celestial sphere. Nevertheless, sidereal time is defined in terms of the vernal point and the term "sidereal" is not strictly accurate. Further distinctions exist between apparent and mean sideral time, but this is beyond the scope of this page and does not affect the basic facts surrounding the equation of time. Details can be found in ESAA [1, pp. 77–78].
Sidereal time is preferred by astronomers. Before the advent of modern technologies, they would use pendulum clocks synchronized with the culmination of a reference star to evaluate the sidereal time of their observations. As long as the position of the reference star with respect to the vernal point is known (at least the angle between their meridian planes), the clock can be adjusted so that 0 hours corresponds to the culmination of the vernal point.
The rotation of the celestial sphere, or of the earth on its axis in the Copernician view, is a very uniform motion. It accords well with other reference periodic phenomena such as the oscillations of a pendulum. It was used until the 1960's as the basis for the definition of the independent time variable of the equations of Newtonian mechanics. By then, it was discovered that the rotation is slowing down and that a better time scale was needed.
Equatorial coordinates
The angle between the meridian planes of the vernal point and a star, measured from west to east (unlike the hour angle), is known as the right ascension of the star. It can be measured along the celestial equator. Like the hour angle, it is measured in hours, minutes, seconds or decimal hours.
The declination of the star, on the other hand, is the angle between the celestial equator and the star, measured along the star's meridian, the intersection of its meridian plane with the celestial sphere. The declination is positive for stars to the north of the equator and negative to the south.
The right ascension (α) and declination (δ) are the equatorial coordinates of the star. Right ascension and declination constitute a coordinate system on the celestial sphere, similar to the geographical coordinate system of longitudes and latitudes used on earth. Equatorial coordinates apply of course to any point of the celestial sphere, not just stars.
True solar time
The sun can also be used as reference object for the measurement of time. Its hour angle measures (local) solar time, more precisely true solar time (the nuance will be explained below). This is the quantity read by a sundial.
Solar time differs from sidereal time because the position of the sun on the celestial sphere is not constant with respect to the background stars. The sun appears to move along a great circle of the celestial sphere called the ecliptic, completing a whole turn in a year (that is the definition of the year, the notion of sidereal year anyway). The sun progresses every day by about 1 degree of arc along the ecliptic (360 degrees in about 365 days), from west to east.
The motion of the sun along the ecliptic causes solar time to shift with respect to sidereal time by about 4 minutes every day (24 hours in about 365 days). A solar day is longer than a sidereal day, because the celestial sphere has to rotate a little more to bring the sun back to the meridian than it would have to do for a star.
In the Copernician model, the motion of the sun along the ecliptic results from the revolution of the earth around the sun. A solar day is longer than a sidereal day because the earth has to rotate a little more every day with respect to the stars in order to catch up with the sun.
If sidereal time were used as a standard for civil time, daylight and our biorythms would slowly shift with respect to the clock, which could be confusing. It makes more sense to use solar time as reference for civil time.
Non-uniformity of true solar time
The difference between true solar time and sidereal time is the difference between the hour angle of the sun and the hour angle of the vernal point, which is precisely the right ascension of the sun.
If the right ascension of the sun varied uniformly (with respect to a sidereal clock) over the course of a year, it would be sufficient to change the length of the second (by changing the length of the pendulum, for instance) to transform a sidereal clock into a solar clock. However this variation is not uniform, for two independent reasons: the inclination of the ecliptic with respect to the celestial equator, and the non-uniformity of the motion of the sun along the ecliptic.
Inclination of the ecliptic
The plane of the ecliptic makes an angle of about 23.5° with respect to the equatorial plane. The ecliptic intersects the celestial equator at the equinoctial points where the sun lies at the equinoxes: the vernal point and the autumnal point corresponding respectively to the spring and fall equinoxes in the northern hemisphere.
In the heliocentric view, the inclination of the ecliptic is the complement of the angle between the axis of the earth and the plane of its orbit around the sun.
The motion of the sun along the ecliptic translates into a variation of its right ascension (through its projection onto the celestial equator along meridians) and a variation of its declination (its height above or below the equator). The variation in declination causes the seasons (when the sun is north of the celestial equator, for instance, it provides more heat to the northern hemisphere by staying longer and rising higher above the horizon) but it does not not affect solar time. Solar time is only affected by the variation in right ascension.
Even if the sun moved along the ecliptic uniformly (which it does not, see below), its right ascension would not vary uniformly, because of the inclination of the ecliptic. This is easily understood by comparing the situations at the solstices and the equinoxes. Around the solstices, the ecliptic is almost parallel to the equator on the celestial sphere, and an angular displacement along the ecliptic projects onto almost the same displacement along the equator. Around the equinoxes, on the other hand, the ecliptic makes its steepest angle of about 23.5° with the equator and a given displacement along the ecliptic projects onto a shorter displacement along the equator (the ratio being the cosine of 23.5°).
This shows that, assuming a uniform motion of the sun along the ecliptic, the variation of the sun's right ascension cannot be uniform. It is faster around the solstices and slower around the equinoxes.
Eccentricity
The motion of the sun along the ecliptic over the course of a year is not uniform either.
The ancients, as early as Hipparchus (c. 190–c. 120 BCE), were well aware of this fact, from the simple observation that the time elapsed between a spring equinox and the following fall equinox (approximately 186 days, 14 hours, 20 minutes) differs from the time elapsed between the fall equinox and the following spring equinox (approximately 178 days, 18 hours, 29 minutes), while these points are separated by 180° on the ecliptic.
Since their cosmological model assumed that the sun traveled on a circle around the earth at uniform velocity, they had concluded that the earth was not positioned at the center of this circle but eccentric with respect to it (Delambre [4, p. 5]), among other features of the model.
Around 1605, Johannes Kepler discovered his first two laws of planetary motion. The first law states that the orbit
of a planet around the sun in an ellipse, with the sun at a focus. The second law states that the motion is such that
"equal areas are swept in equal times" by the planet's radius vector from the sun, or in other words that
the rate or area swept by the radius vector with respect to time is constant. The relative motion of the sun with
respect to the planet follows the same laws.
This implies that the angular velocity of the sun as seen
from the planet must increase or decrease as the planet comes nearer to or moves further from it. Since the earth is
closer to the sun during the (northern) winter months, reaching the perihelion around January 3, Kepler's second law
explains the difference between the times elapsed between equinoxes.
Mean solar time
This makes true solar time inadequate as a time standard. Solar days do not all have the same length (with respect to phenomena more trusted as uniform such as the oscillations of a pendulum or sidereal time) and a "solar second" based on a subdivision of the solar day would stretch or shrink depending on the seasons.
Hence the idea of a mean sun, a fictitious object related to the actual sun but moving uniformly along the celestial equator (rather than the ecliptic), that would be used as reference object for an astronomical time scale, with the advantages of solar time over sidereal time but without its drawbacks.
The notion of mean sun was already familiar to the ancient Greek astronomers (Hipparchos, Ptolemy). It is now rigorously defined as follows (Meeus [2, p. 183], Smart [3, pp. 139–140]) in two steps.
- A first fictitious object, that we may call uniform sun for lack of a standard term, travels along the ecliptic with constant angular velocity and coincides with the true sun at the perigee and apogee.
- A second fictitious object, the mean sun, travels along the equator with constant angular velocity and coincides with the uniform sun at the equinoctial points.
The mean sun is the reference object used to define mean solar time. Then local mean (solar) time (LMT) at some location on earth is the hour angle on the mean sun. By choosing a reference meridian, a global time scale can be established, such as Greenwich mean (solar) time (GMT).
Universal time (UT) and civil time scales were initially based on GMT, with the day starting at midnight rather than (mean) noon. In the 1960's, the discovery of the unpredictable slowing down of the earth's rotation led to the introduction of additional time scales considered more uniform. The whole story is told in ESAA [1, pp. 9–14 and Chapter 3].
The equation of time
We can finally come to the point. The equation of time is by definition the difference between true solar time and mean solar time. For instance, if a mean solar clock shows 3hrs 23min and at the same instant a true solar clock (maybe a sundial) shows 3hrs 31min, then the equation of time at that instant is 8min. The word equation in this context means "the value that needs to be added to one quantity to make it equal to the other", which is not the sense in has acquired in algebra.
According to our definitions, the equation of time is therefore the difference between the hour angles of the true sun and the mean sun. Equivalently, it is the difference between the right ascensions of the mean sun and the true sun.
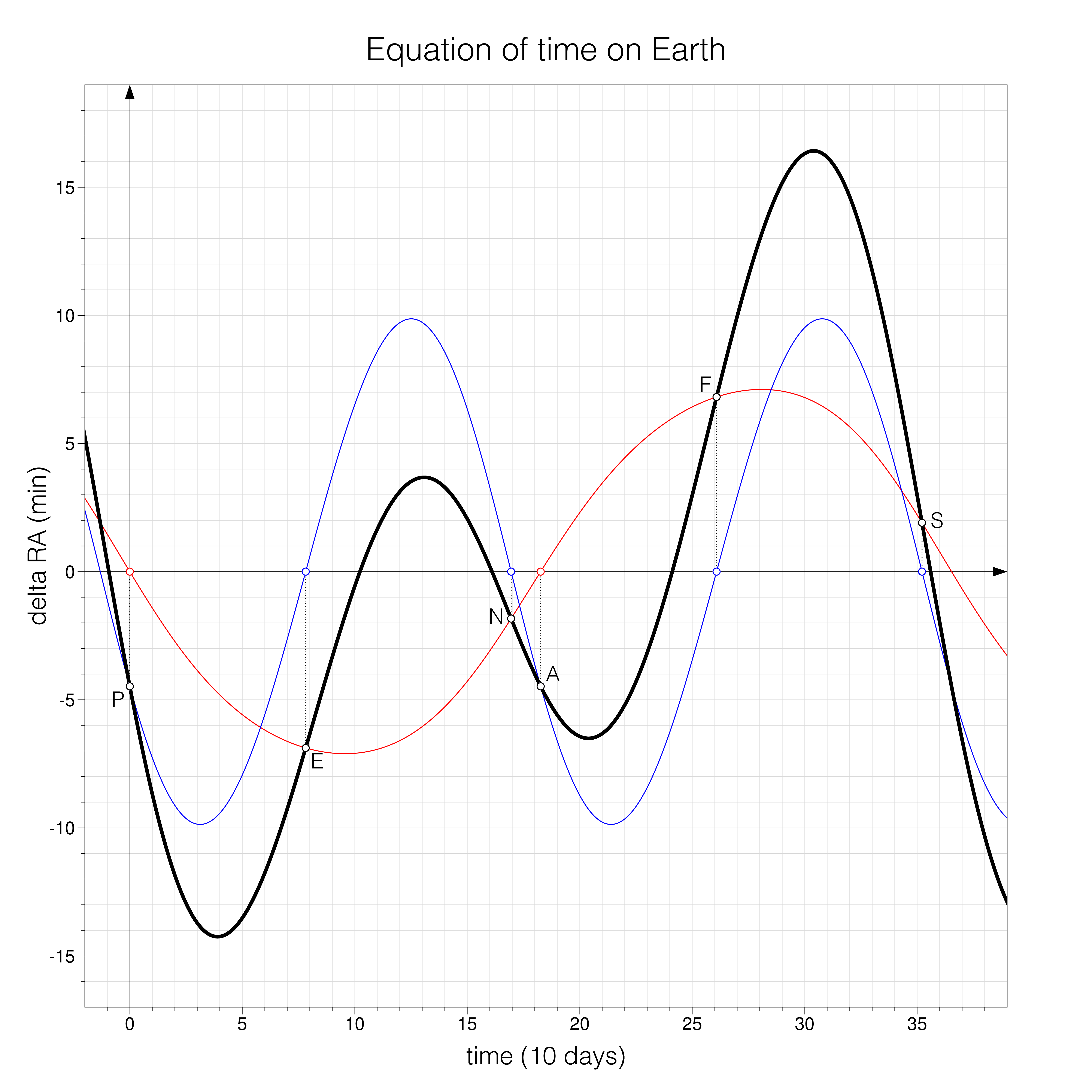
The first diagram shown at the top of the page, repeated here for convenience, represents the equation of time as a function of the day of the year, starting at the perigee (the black curve).
The other curves represent the individual contributions of the obliquity (the difference between "uniform solar time" and mean solar time, in blue), and the eccentricity of the orbit (the difference between true solar time and uniform solar time, in red). The ordinate of every point on the black curve is the sum of the ordinates of the points on the other curves at the same abscissa.
The special points on the curves mark the situations
- at the perigee (P) and apogee (A), where the true and uniform suns coincide and there is no difference between true and uniform solar times,
- at the equinoctial points, vernal (E) and autumnal (F), where the uniform and mean suns coincide and there is no difference between uniform and mean solar times,
- at the north (N) and south (S) solstitial points where the uniform and mean suns coincide again and there is no difference between uniform and mean solar times.
Note that the instants corresponding to the points (E) (F) (N) (S) are the times of passage of the uniform sun at the equinoctial and solstitial points on the relative orbit of the sun. The true sun does not necessarily pass through these points at exactly the same time.
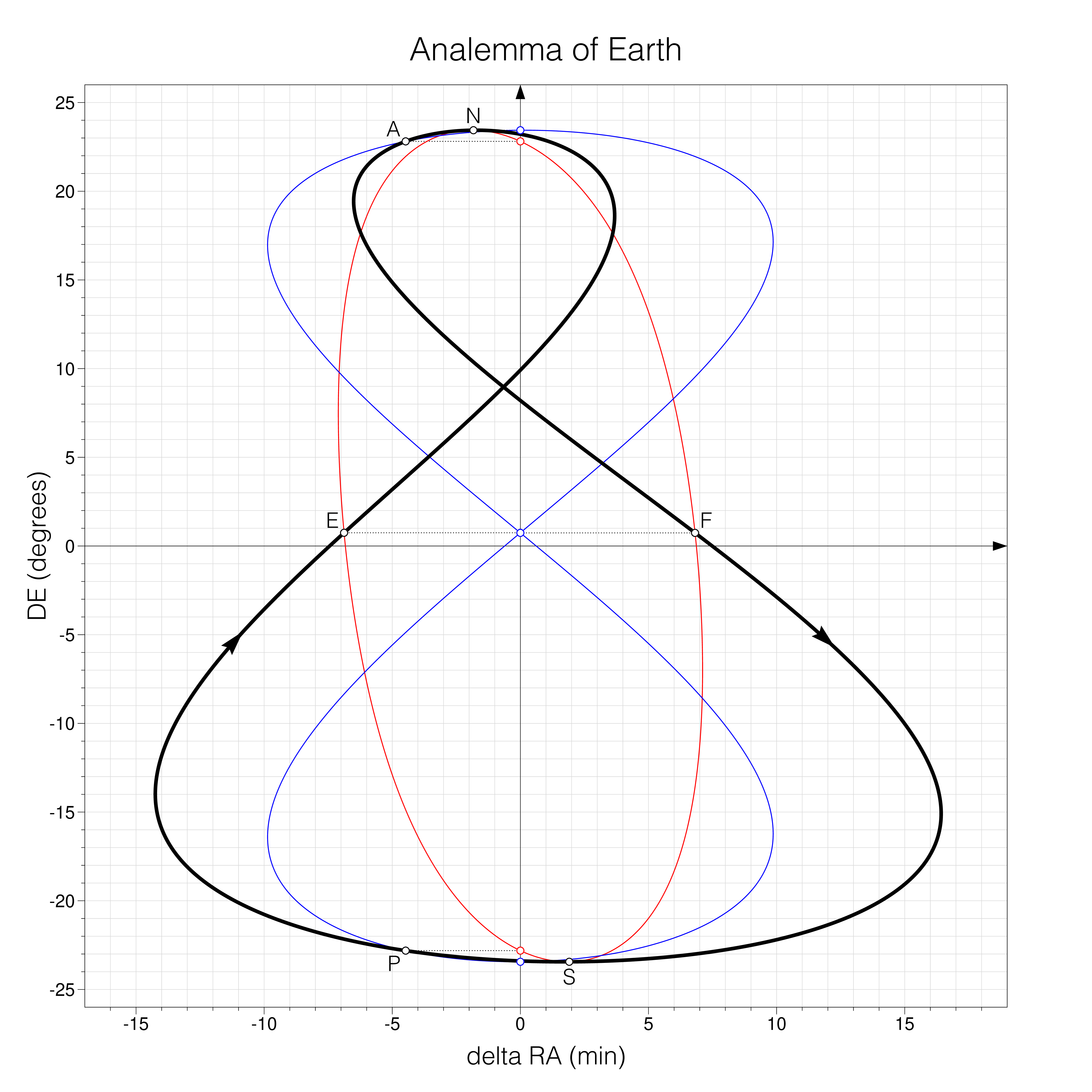
The analemma
The analemma is the curve obtained by plotting the equation of time as the x coordinate against the declination of the (true) sun as the y coordinate.
At each instant, the declination of the sun and value of the equation of time correspond to a point on the curve. This point moves along the curve as the sun moves along the ecliptic, in the direction indicated by the arrow on the black curve, completing a full turn in a year.
Again, the individual contributions of the obliquity (in blue) and the eccentricity (in red) are represented, as well as the situation at the perigee (P), apogee (A), vernal (E) and autumnal (F) points, north (N) and south (S) solstitial points. The abscissa of any point of the black curve is the sum of the abscissas of the points of the blue and red curves at the same ordinate (and chosen on the correct branch of the curve, the one corresponding to the same season, since in most cases two abscissas correspond to the same ordinate on each curve).
This particular way of plotting the equation of time makes it convenient to compute mean solar time from the reading on a sundial. The sundial may give the declination of the sun as the length of the shadow of the stylus, in addition to true solar time. The time correction, the equation of time, can be read directly on the analemma curve at that declination. For this reason, the analemma curve can sometimes be found drawn on the face of sundials.
Equation of time and analemma on other planets
The shape of a planet's orbit and the relative position of its rotation axis affect the appearance of the equation of time and analemma curves in surprising ways. The curves associated with the other planets of the solar system (and Pluto) are shown below.
Mercury
|
Venus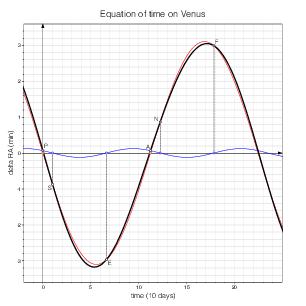
|
Mars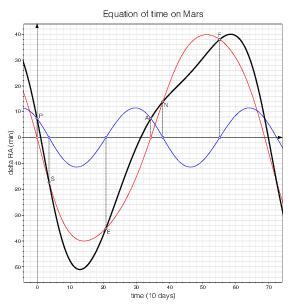
|
Jupiter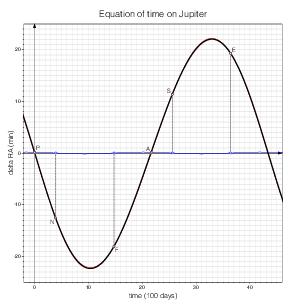
|
Saturn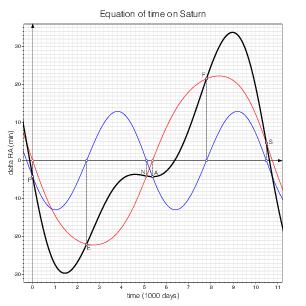
|
Uranus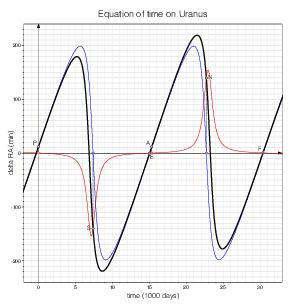
|
Neptune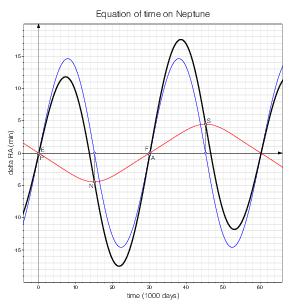
|
Pluto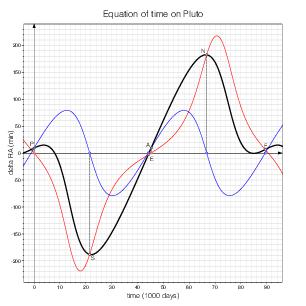
|
Mercury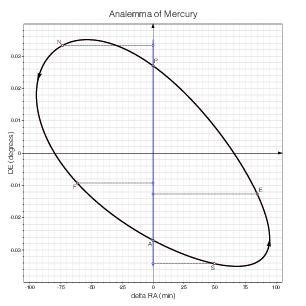
|
Venus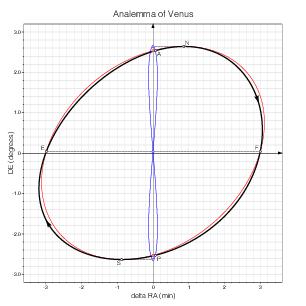
|
Mars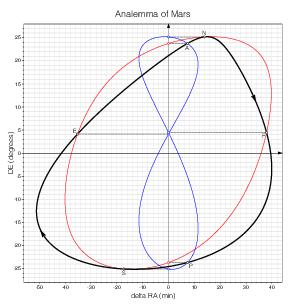
|
Jupiter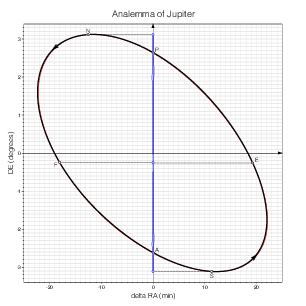
|
Saturn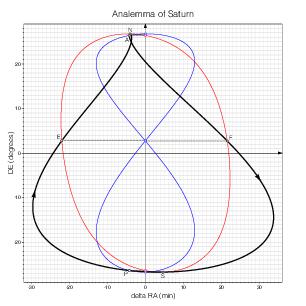
|
Uranus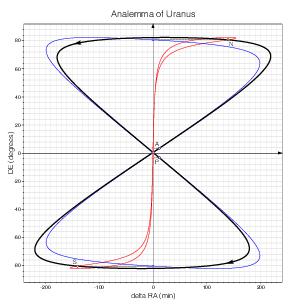
|
Neptune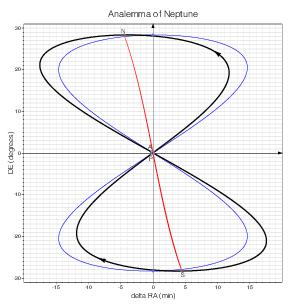
|
Pluto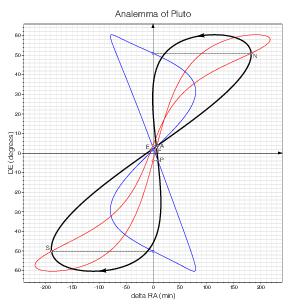
|
I have computed these curves on the basis of the Keplerian Elements for Approximate Positions of the Major Planets in ESAA [1, pp. 338–341] and the positions of the poles of the planets in ESAA [1, Table 10.1, p. 402]. The curves correspond to the orbital elements and poles as of J2000.
In fact, the orbital elements and poles vary over time, and the shapes of the curves slowly change accordingly. This simplified model omits other fine details too, but it suffices for the purpose of this page.
References
[1] S. E. Urban & P. K. Seidelman, Eds., Explanatory Supplement to the Astronomical Almanac, 3rd Edition, Mill Valley: University Science Books, 2013.
[2] Jean Meeus, Astronomical Algorithms, 2nd Edition, Richmond, VA: Willmann-Bell, Inc., 1999.
[3] W. M. Smart, Textbook on Spherical Astronomy, 6th Edition revised by R. M. Green, Cambridge: Cambridge University Press, 1977.
[4] Jean-Baptiste Joseph Delambre, Astronomie Théorique et Pratique, Tome II, Paris: Courcier, 1814.